برهان غیرمستقیم اعتبار (برهان خلف)
روشهای استنتاج
درآمد به منطق فصل ۱۰ قسمت ۱۱
در قسمت پیشین، روش (قاعده) برهان شرطی در برهان آوری برای استدلال را دیدیم و آن را به جعبه ابزار منطقی خود افزودیم. افزون بر قاعده برهان شرطی روشی (قاعدهای) دیگر و کارآمد مشهور به «برهان غیرمستقیم اعتبار» (برهان خلف) برای اثبات اعتبار استدلال وجود دارد که میتوان آن را نیز به جعبه ابزار منطقی خود بیافزایم. در برهان خلف باید با فرض نقیض گزاره مورد اثبات و کارزدن قواعد استنتاج صرفاً به این فرض یا ترکیب عطفی آن با مقدمه
(مقدمات) به یک تناقض صریح
(مانند q•~q) رسید. در این قسمت به معرفی و توضیح این روش برهان آوری میپردازیم.
جای دارد اینجا، یک نکته یادآوری شود، و آن اینکه، نیز رسم است برای اثبات اعتبار یک استدلال، نقیض نتیجه آن را فرض گرفته و سپس به نقیض مقدمه (یا عطف مقدمات) رسیده، این روش در واقع یک برهان مستقیم است (ترکیبِ برهان شرطی و قاعده عکس نقیض) و نه یک برهان غیرمستقیم.
۱۱.۱۰ برهان غیرمستقیم اعتبار (برهان خلف)
در این قسمت، برهان غیرمستقیم (I.P.)، دومین روش بسیار توانمند برهان آوری را معرفی کرده و آن را توضیح میدهیم. در یک برهان غیرمستقیم (نیز مشهور به برهان خُلف)، یک گزاره، ~p (یا p) را فرض میکنیم، آنگاه یک تناقض با صورت q•~q را بهدست میآوریم، سپس بهطور معتبر نقیض فرض خود، یعنی p (یا ~p) را اندریافت میکنیم. دو صورت استدلال فرضی برای یک برهان غیرمستقیم عبارتند از:
~p ... ... ... q • ~q | /∴ q (I.P. فرض) | p ... ... ... q | /∴ q (I.P. فرض) q • ~q |
| p | I.P. | ~q | I.P. |
در برهان غیرمستقیمِ اعتبار، به جای اینکه مستقیماً از مقدمات با استنتاجهای معتبر به نتیجه برسیم، بهطور غیرمستقیم از طریق یک تناقض به نتیجه میرسیم؛ و از این جهت است که غیرمستقیم است. استنتاج یک تناقض در برهان غیرمستقیم ضروری است، حال آنکه، در برهان مستقیم هیچ تناقضی بیرون آورده نمیشود.
آ. توضیح و موجه کردن برهان غیرمستقیم
برهان غیرمستقیم اعتبار
برهان خلف
تعلیق به محال
کاهش به پوچی
Indirect Proof
reductio ad absurdum
برهانی که در آن برای اثبات، نقیضِ گزاره (مانند ~p) یا گزارهای (مانند p) که باید اثبات شود، را فرض گرفته، و سپس یک تناقض صرفاً از آن فرض یا از ترکیب عطفی آن فرض و مقدمات بهدست آورده میشود. هنگامی که تناقض استنتاج شد، این فرض تخلیه شده و نقیض فرض بطور استنتاجی اندریافت میشود. برای مثال، اگر ~p در خط (محدوده) قلمرو خود فرض شود، یک تناقض با صورت q•~q استنتاج میشود. سپس این فرض تخلیه شده، و آنگاه نقیض فرض اصلی یعنی p اندریافت میشود.
از روش برهان غیرمستقیم میتوان برای اثبات اعتبار هر استدلال معتبر استفاده کرد. برای درک اینکه چرا چنین است، باید یادآور شویم که یک استدلال معتبر نمیتواند دارای همهیِ مقدماتِ درست و نتیجهیِ نادرست باشد. بنابراین، یک استدلال
P۱
P۲
∴ C
معتبر است اگر و تنها اگر ترکیب عطفی مقدمات آن و نقیض نتیجه آن (یعنی نادرستی نتیجه آن) یک تناقض باشد.
(P۱ • P۲) • ~C
در این نکته که گفته شد، موجه بودنِ برهان غیرمستقیم نهفته است. اگر نادرستییِ نتیجهیِ استدلال (یعنی نقیض آن) را فرض بگیریم و بطور معتبر از مقدماتِ استدلال و آن فرض، یک تناقض صریح را استنتاج کنیم، آنگاه ثابت کردهایم استدلال معتبر است، زیرا تناقض بهدست آمده ثابت میکند که استدلال نمیتواند همهیِ مقدمات درست و نتیجهیِ نادرست را داشته باشد.
| ۱. | P۱ | |
| ۲. | P۲ | /∴ C |
| ۳. | ~C | /∴ (I.P فرض) |
| ۴. | .... | |
| ۵. | .... | |
| ۶. | q • ~q | |
| ۷. | C | ۳ - ۶, I.P. |
برای فهم کامل اینکه چگونه برهان غیرمستقیم (I.P.) اعتبار هر استدلال را اثبات میکند، باید بدانیم، اگر یک استدلال معتبر باشد آنگاه ترکیب عطفی مقدمات آن و نقیض نتیجه آن، یعنی (P۱•P۲)•~C، میتواند به سه حالت متمایز یک تناقض باشد.
| (آ) | (P۱•P۲)•~C یک تناقض است چون | ~C | متناقض با P۱•P۲ است. | مقدمات سازگار و نتیجه ممکن. |
| (ب) | (P۱•P۲)•~C یک تناقض است چون | ~C | یک تناقض است. | نتیجه یک توتولوژی است. |
| (ج) | (P۱•P۲)•~C یک تناقض است چون | P۱•P۲ | یک تناقض است. | مقدمات ناسازگار هستند. |
ترکیب عطفیِ (P۱•P۲)•~C به سه طریقِ متمایز میتواند یک تناقض باشد زیرا استدلالها به سه طریقِ متمایز میتوانند معتبر باشند:
| (آ) | یک استدلال معتبر با مقدمات سازگار و یک نتیجهیِ ممکن میتواند همه مقدمات آن درست و نتیجهیِ نادرست باشد، اما نمیتواند دارایِ همهیِ مقدمات درست و هم دارایِ نتیجهیِ نادرست باشد، زیرا درستیِ نتیجهیِ آن در درونِ (یا لازمشده توسط) درستیِ مقدمات آن است (استدلال VI در ادامه). |
| (ب) | یک استدلال معتبر با یک نتیجه توتولوژیک نمیتواند دارای همهیِ مقدمات درست و نتیجه نادرست داشته باشد، زیرا ممکن نیست چنین استدلالی نتیجهیِ نادرست داشته باشد (استدلال VII در ادامه). |
| (ج) | یک استدلال معتبر با مقدمات ناسازگار نمیتواند دارای همهیِ مقدمات درست و یک نتیجه نادرست باشد، زیرا نمیتواند دارای همهیِ مقدمات درست باشد (استدلال VII در ادامه). |
اکنون و به نوبت به هر یک از این موارد نگاه میکنیم تا ببینیم چگونه یک برهان غیرمستقیم بهطور معتبر در هر یک از آنها یک تناقض را نتیجه میگیرد و بدین وسیله اعتبار یک استدلال را اثبات میکند.
ابتدا مورد (آ) در بالا را در نظر بگیرید. به یاد داشته باشید که گزارههای متناقض هر دو نمیتوانند درست باشند. بنابراین، اگر یک گزاره ممکن را به مجموعهای از مقدمات سازگار اضافه کنیم و بتوانیم تناقضی را استنتاج کنیم، نقیض آن فرض افزونتر باید بهطور معتبر از مقدمات ناشی شود. برای مثال، استدلال معتبر زیر را در نظر بگیرید.
(P۱): F ⊃ GVI استدلال
(P۲): F
∴ G
اگر بهعنوان یک فرض اضافی، نقیض نتیجه، یعنی ~G را اضافه کنیم، میتوانیم تناقض را به قرار زیر استنتاج کنیم:
تناقضِ، F•~F، از ترکیب عطفی دو مقدمه و فرض I.P.، یعنی ~G، قابل استنتاج است، زیرا ~G با دو مقدمهیِ سازگارِ اصلی در تناقض است. اینکه ~G با دو مقدمه در تناقض است در این واقعیت آشکار است که G را میتوان (مستقیماً) در خط ۴ توسط M.P. استنتاج کرد، که امکان استنتاج یک تناقض متفاوت، یعنی G•~G را فراهم میکند.
| ۱. | F ⊃ G | |
| ۲. | F | /∴ G |
| ۳. | ~G | /∴ (I.P فرض) |
| ۴. | ~G | ۱, ۲, M.P |
| ۵. | G • ~G | ۴, ۳, Conj. |
این برگرفتن به صراحت نشان می دهد که استنتاج F•~F در مورد اول فقط به این دلیل امکانپذیر است که G بهطور معتبر از دو مقدمه سازگار اصلی بهدست میآید - یعنی فقط به این دلیل که ~G با عطف مقدمات در تناقض (F⊃G)•F است.➥۲۶
درستی ~G با مقدمات در تناقض است زیرا درستی G در درستی ترکیب عطفی مقدمات (F⊃G)•F (یا لازم شدهیِ آن) است. به عبارت دیگر، ترکیب عطفی مقدمات، (F⊃G)•F ، تنها در صورتی درست است که G درست باشد.بنابراین، در خط ۶ میتوان بهطور معتبر G، نقیض فرض I.P. یعنی ~G، را از دو فرض اصلی توسط برهان غیرمستقیم استنتاج کرد.
۶ G ۳ - ۵, I.P.
این موجه کردن که در بالا آمد در مورد اکثریت قریب به اتفاق استدلالهای معتبر در این کتاب، که نتایج ممکن آنها بهطور معتبر از مقدمات سازگار بهدست میآید، به کار زده خواهد شد.
حالت بعدی (ب) را در بالا را در نظر بگیرید. هر استدلال با نتیجه توتولوژیک معتبر است: چنین استدلال نمیتواند دارای همهیِ مقدماتِ درست و نتیجهیِ نادرست باشد زیرا نتیجهیِ آن نمیتواند نادرست باشد.➥۲۷
بخش ۱۰.۱۳ را برای بحث در مورد استدلال های معتبر با نتایج توتولوژیک ببینید.برای مثال، استدلال زیر معتبر است، زیرا، گرچه مقدماتِ سازگار آن میتوانند همه درست باشند، اما نتیجه توتولوژیک آن نمیتواند نادرست باشد.
(P۱): F ⊃ GVII استدلال
(P۲): F
∴ H ∨~H
اگر مقدمات را با اضافه کردن، بهعنوان یک فرض اضافی، نقیض این نتیجه توتولوژیک افزایش دهیم، میتوانیم یک تناقض بهقرار زیر استنتاج کنیم.
از آنجا که ما یک تناقض را از مقدمات سازگار و نیز یک فرض اضافه استنتاج کردهایم، پس میتوانیم بهطور معتبر نقیض فرض خود، یعنی H∨~H را استنتاج کنیم.
۷. H ∨ ~H ۳ - ۶, I.P.
برخلاف استدلال VI، فرض اضافهشدهِ I.P. ،~(H∨~H) ، با دو مقدمه سازگار اصلی در تناقض نیست. در عوض، ~(H∨~H) استنتاج یک تناقض با صورت ~(H∨~H) را امکانپذیر میکند زیرا ~(H∨~H) خود یک تناقض است. از آنجا که نقیض توتولوژی یک تناقض است، بنابراین اگر نقیض هر توتولوژی را به مقدمات سازگار (یا ناسازگار) اضافه کنیم، میتوانیم تناقضی را به صورت الگوی ~(q•~q) تنها از نقض توتولوژی استنتاج کنیم. ما در اینجا تناقض H•~H را از فرض I.P.، یعنی ~(H∨~H)، به تنهایی استنتاج کردهایم، که نشان میدهد، نقیض این فرض، H∨~H، بهطور معتبر از مقدمات سازگار نتیجه میشود.
آنچه که استدلالهای VI و VII نشان میدهند این است که هرگاه یک فرض اضافی به مقدمات سازگار اضافه شود و تناقضی استنتاج شود، نقیض آن فرض اضافی بهطور معتبر از آن مقدمات ناشی میشود. این کاربرد I.P. همهیِ استدلالهای معتبر با مقدمات سازگار را موجه میکند.
سرانجام، آنچه هنوز باقی است، اینکه ما باید کارزدن I.P. را، در برهان اعتبار استدلالهای دارای مقدمات ناسازگار، موجه سازیم. توجیه لازم برای حالت (ج)، در بالا، به آسانی قابل ارائه است، زیرا همانطور که از قسمت ۱۰.۱۰ میدانیم، هر استدلالی با مقدمات ناسازگار معتبر است: استدلالی با مقدمات ناسازگار نمیتواند دارای همه مقدمات درست و نتیجه نادرست باشد. برای مثال، استدلال زیر را در نظر بگیرید:
(P۱): F ⊃ GVIII استدلال
(P۲): F
(P۳): ~G
∴ R
ما میتوانیم بهعنوان یک فرض اضافی I.P. نقیض نتیجه، یعنی ~R را افزوده و یک تناقض را به صورت زیر استنتاج کنیم.
پس از استنتاج یک تناقض از مقدمات ناسازگار، میتوانیم بهطور معتبر نقیض فرض ما، یعنی R، را بهدست آوریم.
۷. R ۴ - ۶, I.P.
در این حالت، جایی که مقدمات خود ناسازگار هستند، میتوانیم نقیض هر گزارهای را اضافه کنیم و یک تناقض را استنتاج کنیم، نه به این دلیل که فرض افزوده با مقدمات در تناقض است (مانند استدلال VI) و نه به این دلیل که فرض افزوده خود یک تناقض است (مانند استدلال VII). بلکه به این دلیل که خودِ مقدمات ناسازگار هستند. از آنجا که، هر عبارت-گزارهای، مانند R، از مقدمات ناسازگار ناشی میشود، ممکن است نقیض R، یعنی ~R را فرض کنیم، آنگاه تناقضی را تنها از مقدمات استنتاج کنیم و سپس بطور معتبر R را بهدست آوریم.
ب. روند برهان غیرمستقیم
اکنون روند کلی برای برهان غیرمستقیم را نشان میدهیم.
پیش از ادامه این بند و برای دسترسی دو صورت استدلال فرضی برای یک برهان غیرمستقیم، که در ایتدای این قسمت آمده است، را نیز اینجا میآوریم:
~p ... ... ... q • ~q | /∴ q (I.P. فرض) | p ... ... ... q | /∴ q (I.P. فرض) q • ~q |
| p | I.P. | ~q | I.P. |
برهان غیرمستقیم اعتبار (یا برهان خلف) [نیز «کاهش به پوچی» یا «تعلیق به محال»] با نوشتن یک فرض افزوده در سمت راست یک خط قلمرو جدید،➥
۲۸- در بخش (د) خواهیم دید که میتوان با فرض نقیض آن گزاره، توتولوژی بودن یک گزاره را ثابت کرد. در چنین حالتی، ثابت میشود که گزاره یک توتولوژی است. به عبارت دیگر، شخص ثابت نمیکند که استدلالی معتبر است و از فرض I.P بعنوان یک مقدمه اضافی استفاده نمیشودنقیض گزارهای که میخواهیم استنتاج کنیم، یعنی ~p، (یا فرض p، اگر بخواهیم ~p را استنتاج کنیم) آغاز میشود.➥
۲۹- تمرینات (آ) ۴، ۲ و (ج) ۶ را ببینید، جایی که نتیجه به ترتیب G~ و R~ و ~O است. نیز میتوانیم نقیض نتیجه استدلال را فرض بگیریم. همچنین در هر زمان، نقیض هر گزارهای که میخواهیم استنتاج کنیم، را فرض کنیم. اگر بتوانیم تناقض صریح با صورت q•~q را از مجموعه مقدماتی که بدین ترتیب افزودهایم استخراج کنیم، میتوانیم بهطور معتبر فرض I.P. را نقض کنیم. در موردی که فرض I.P. نقیض نتیجه استدلال است، در واقع ثابت میکنیم، استدلالی را که با آن شروع کردهایم معتبر است. روش برهان غیرمستقیم استدلال در زیر نشان داده شده است:
۱. A ⊃ (B • C)
۲. (B ∨ D ) ⊃ E
۳. D ∨ A /∴ E
در خط بعدی، برهان I.P. خود را با نوشتن فرض I.P.، یعنی ~E، نقض نتیجه، در ستون عبارتهای-گزارهای، در سمت راست یک خط قلمرو جدید آغاز میکنیم. اکنون که سرشت فرضِ برهان غیرمستقیم بر ما کاملاً آشکار است، از این پس بجای «فرض A.I.P.» کوتاه شده آن را با عنوان "A.I.P." مینویسیم.
۴. E /∴ (A.I.P.)
در ستون توجیهی، «/(A.I.P.)» را مینویسیم تا نشان دهیم گزاره ~E یک فرض I.P. است. با مجموعه مقدماتی که اکنون گسترش یافته است، میتوانیم با استفاده از قواعد استنتاج تعیین شده، یک تناقض صریح را استنتاج کنیم و سپس بهطور معتبر نتیجه مطلوب E را استنتاج کنیم.
| ۵. | ~(B ∨ D) | ۲, ۴, M.T. |
| ۶. | ~B • ~D | ۵, DeM. |
| ۷. | ~D • ~B | ۶, Com. |
| ۸. | ~D | ۷, Simp. |
| ۹. | A | ۳, ۸, D.S |
| ۱۰. | B • C | ۱, ۹, M.P |
| ۱۱. | B | ۱۰, Simp. |
| ۱۲. | ~B | ۶, Simp. |
| ۱۳. | B • ~B | ۱۱, ۱۲, Conj. |
| ۱۴. | E | ۴ - ۱۳, I.P |
خط قبل از آخرین خط در برهان دربردارِ یک تناقض صریح است، B•~B، که نمایانگر از پوچیای است که با فرض ~E در خط ۴ بدان سوق داده شدیم. این تناقض نشان میدهد که E بطور معتبر از مقدمات نتیجه میشود و نمایان میکند که پیوند عطفی مقدمات و ~E یک تناقض است. برهان غیرمستقیم با تخلیه فرض I.P. (یعنی پایان دادن به خط قلمرو) و استنتاج نقیض فرض I.P.، یعنی E، در آخرین خط برهان پایان مییابد. در ستون توجیهی، محدودهیِ قلمرو سطرهای برهانِ غیرمستقیم (برای مثال، در این مورد، سطرهای "۱۳-۴") و به دنبال آن "I.P." آورده شده است.
از آنجا که، روش برهان غیرمستقیم به یک تناقض (مهمل - پوچی) منجر میشود، به آن «کاهش به پوچی» (یا «تعلیق به محال» - "reductio ad absurdum" - نیز میگویند. روش برهان غیرمستقیم در برخی شرایط، امکان اثبات اعتبار سریعتر از آنچه که بدون آن ممکن است، را ممکن میکند. ما میتوانیم این را ابتدا با ساختن یک برهان صوری مستقیم برای اعتبار یک استدلال، و سپس نشان دادن اعتبار همان استدلال با استفاده از یک برهان غیرمستقیم، توضیح دهیم. در مثال زیر، برهان مستقیم که در سمت چپ است، به ۱۵ سطر نیاز دارد. برهان غیرمستقیم که فقط به ۸ خط نیاز دارد در سمت راست است. مانند برهان شرطی، از یک خط قلمرو برای نشان دادن قلمرو یک برهان غیرمستقیم استفاده میشود.

خط قلمرو در یک برهان غیرمستقیم مانند خط قلمرو برای برهان شرطی عمل میکند: عبارتهای-گزارهای استنتاج شده در یک خط قلمرو را نمیتوان پس از تکمیل زیر-برهان و پایان خط قلمرو در اندریافتها به کار گرفت.
ج. زیر-برهانهایِ غیرمستقیمِ تو در تو
برهانهای غیرمستقیم زمانی میتوانند سازنده باشند که درون یک برهان شرطی یا در برهان غیرمستقیمِ تودرتو باشند.➥۳۰ استدلال زیر را در نظر بگیرید.
(P۱): C ⊃ (M ⊃ D)
(P۲): D ⊃ V
(P۳): (D ⊃ A) • ~A
∴ M ⊃ ~C
اعتبار این استدلال در زیر با یک I.P. تودرتو که خود درون یک برهان C.P. است ثابت شده است.
| ۱. | C ⊃ (M ⊃ D) | ||
| ۲. | D ⊃ V | ||
| ۳. | (D ⊃ A) • ~A | /∴ M ⊃ ~C | |
| ۴. | M | /∴ ~C (A.C.P.) | |
| ۵. | C | / (A.I.P.) | |
| ۶. | M ⊃ D | ۱, ۵, M.P | |
| ۷. | D | ۶, ۴, M.P | |
| ۸. | D ⊃ A | ۳, Simp. | |
| ۹. | A | ۸, ۷, M.P. | |
| ۱۰. | ~A • (D ⊃ A) | ۳, Com. | |
| ۱۱. | ~A | ۱۰, Simp. | |
| ۱۲. | A • ~A | ۹, ۱۱, Conj. | |
| ۱۳. | ~C | ۵ - ۱۲, I.P | |
| ۱۴. | M ⊃ ~C | ۴ - ۱۳, C.P. | |
مانند یک زیر-برهان شرطی که درون یک برهان شرطی جاسازی شده است، همیشه باید قلمروهای دامنه فرضها (و خطهای قلمرو مرتبط با آنها) را رعایت کرد: نمی توان از یک گزاره فرض گرفته یا استنتاج شده از یک برهان شرطی یا برهان غیرمستقیم خارج از قلمرو آن استفاده کرد (یعنی، بعد از آنکه فرض تخلیه سده است). بنابراین، در برهان بالا، نمیتوانیم از عبارت-گزارهای استنتاج شده M⊃D (سطر ۶) بعد از اینکه فرض برهان غیرمستقیم در سطر ۱۴ تخلیه شد، استفاده کنیم. برای مثال، ما نمیتوانیم
| ۱۵. | M ⊃ V | خطا | ۷, ۲, H.S. |
را استنتاج کنیم.
عبارت-گزارهای M⊃D در سطر ۶ از مقدمات و دو فرض افزوده استنتاج شده است. M⊃D بطور معتبر به تنهایی از مقدمات بهدست نمیآید. بلکه از مقدمات و فرض I.P.، یعنی C،➥۳۱
۳۱- خواننده میتواند از STTT برای تعیین اینکه M⊃D به تنهایی از مقدمات بهدست نمیآید، با اثبات اینکه فرضها میتوانند همه درست باشند و M⊃D میتوانند نادرست باشند، استفاده کنند. بطور مشابه میتوان از STTT برای اثبات اینکه M⊃V بهطور معتبر از محل پیروی نمی کند استفاده کرد. بهدست آمده است. به همین دلیل است که M⊃D (به ضرورت) صرفاً از مقدمات نتیجه نمیشود و نمیتوان آن را در استنتاج، پس از اینکه فرض I.P. برای آن در سطر ۱۳ تخلیه شد، بهکار گرفت. تنها عبارتهای-گزارهای که میتوانند در ستون گزارهها بدون خط قلمرو در کنار آنها ظاهر شوند، مقدمات و آن عبارتهای-گزارهای هستند که بطور معتبر از مقدمات استنتاج شدهاند (یعنی، به شمول عبارتهای-گزارهای که بطور معتبر از سایر عبارتهای-گزارهای از قبل و به تنهایی از مقدمات استنتاج شدهاند). بنابراین، M⊃V نمیتواند در ستون گزارهها بدون خط قلمرو در کنار آن ظاهر شود، زیرا از یک مقدمه (D⊃V، در خط ۲) و عبارت-گزارهای بهدست آمده است که به تنهایی از مقدمات استنتاج نشده است (یعنی M⊃D، در خط ۶).
تمرین
آ. برای هر یک از استدلالهای زیر، یک برهان غیرمستقیم اعتبار بسازید.

ب. برای هر یک از دو استدلال زیر، یک برهان غیرمستقیم اعتبار بسازید.
| ۱- | اگر کاهش شدید نرخ بهره اصلی باعث افزایش در بازار سهام شود، مطمئناً به زودی تورم خواهد آمد. اما اگر کاهش عرضه پول باعث کاهش شدید نرخ بهره شود، تورم اولیه نیز به همان اندازه قطعی است. بنابراین تورم به زودی بر سر ما خواهد آمد. (F, R, I, D) |
| ۲- | اگر سطح بارندگی بدون تغییر باقی بماند و گرمایش جهانی تشدید شود، سطح اقیانوس ها افزایش مییابد و برخی از بنادر اقیانوسها زیر آب میروند. اما در صورت تشدید گرمایش زمین، بنادر اقیانوسی زیر آب نخواهند رفت. بنابراین یا سطح بارندگی بدون تغییر باقی نخواهد ماند یا گرمایش جهانی تشدید نخواهد شد. (L، G، O، P) |
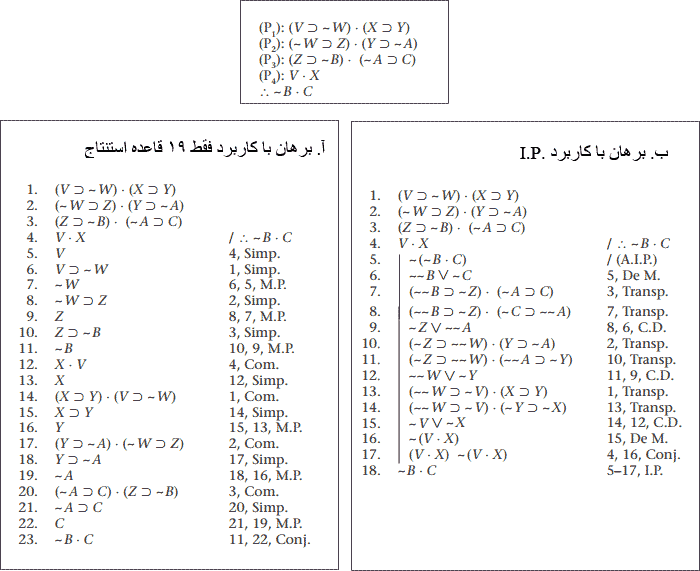
ج. برای استدلال زیر، (الف) برهان صوری مستقیم اعتبار و (ب) برهان غیرمستقیم اعتبار را بسازید. طول دو برهان را با هم مقایسه کنید.
د. برهان غیر مستقیم توتولوژیها
برای اثبات توتولوژیک بودن یک عبارت-گزارهای میتوان از برهان غیرمستقیم استفاده کرد، چرا که اگر عبارت-گزارهای توتولوژی باشد، نقیض آن یک تناقض است. فرض کنید، برای مثال، میخواهیم ثابت کنیم که
G ∨ ~G
یک توتولوژی است. در چنین حالتی، با فرض نقیض آن و استنتاج معتبر یک تناقض صریح، ثابت میکنیم که G∨~G یک توتولوژی است.
بنابراین در آغاز برهانِ I.P.، عبارت-گزارهای ~(G∨~G)، را فرض میگیریم و بطور معتبر از آن تناقض صریح G•~G را استنتاج میکنیم. این ثابت میکند که فرض I.P. اولیه یک تناقض است، که از آن نتیجه گرفته که نقیض آن، G∨~G، یک توتولوژی است. مانند هر برهان غیرمستقیم دیگر، هنگامی که یک تناقض صریح را استنتاج کردیم، همانطور که در سطر ۴ انجام دادهایم، فرضِ I.P. را تخلیه می کنیم و بهطور معتبر نقیض فرضِ I.P. را استنتاج میکنیم.
به همین روش برای اثبات توتولوژیِ
[(M ⊃ Q) • M] ⊃ Q
به شیوه زیر ادامه میدهیم.
| ۱. | ~{[(M ⊃ Q) • M] ⊃ Q} | / (A.I.P.) |
| ۲. | ~{~[(M ⊃ Q) • M] ∨ Q | ۱, .Impl |
| ۳. | ~~[(M ⊃ Q) • M] • ~Q | ۲, .DeM |
| ۴. | [(M ⊃ Q) • M] • ~Q | ۳, .D.N |
| ۵. | (M ⊃ Q) • M | ۴, Simp. |
| ۶. | M ⊃ Q | ۵, Simp. |
| ۷. | M • (M • Q) | ۵, .Com |
| ۸. | M | ۷, Simp. |
| ۹. | Q | ۶, ۸, M.P. |
| ۱۰. | ~Q • [(M ⊃ Q) • M] | ۴, .Com |
| ۱۱. | ~Q | ۱۰, Simp. |
| ۱۲. | Q • ~Q | ۹, ۱۱, Conj. |
| ۱۳. | [(M ⊃ Q) • M] ⊃ Q | ۱ - ۱۲, I.P |
I.P. را میتوان برای اثبات هر توتولوژی بهکار برد، اما، همانطور که در بند (F)، در زیر خواهیم دید، توتولوژیهای شرطی با استفاده از C.P. کارآمدتر اثبات میشوند.
تمرین
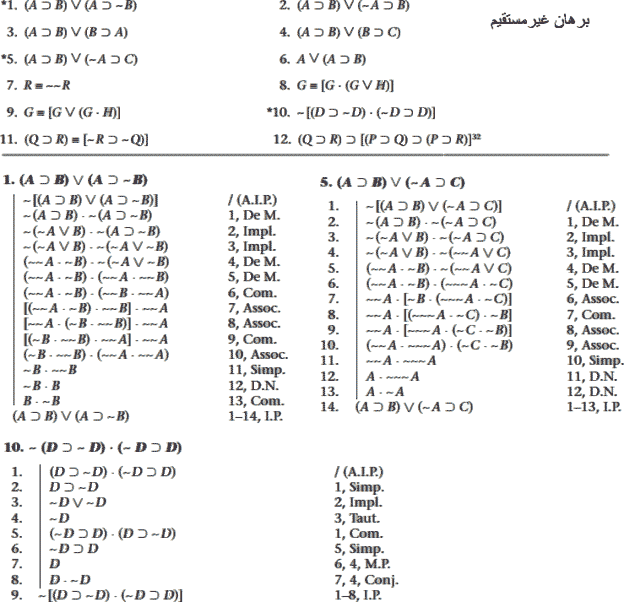
با برهان غیرمستقیم ثابت کنید عبارتهای-گزارهای زیر توتولوژی هستند.
د. افزونگی برهان غیرمستقیم
اگرچه برهانهای غیرمستقیم اندکی کوتاهتر هستند، اما باید دانست که پس از افزودن برهان شرطی به قواعد ۱۹ گانه استنتاج، برهان غیرمستقیم یک افزونگی است.
برای دیدن این، به استدلال زیر نگاه کنید.
(P۱): A ⊃ (B • C)
(P۲): (B ∨ D) ⊃ E
(P۳): D ∨ A)
∴ E
این استدلال را میتوان با استفاده از C.P. ثابت کرد. کلید چنین برهانی این واقعیت است که در بخش ۱۰.۱۰ (ناسازگاری) مورد بحث قرار گرفت، که میتوان هر عبارت-گزارهای را از یک تناقض با کاربرد افزایس و قیاس فصلی استنتاج کرد.
| ۱. | A ⊃ (B • C) | |
| ۲. | (B ∨ D) ⊃ E | |
| ۳. | D ∨ A | ∴ E |
| ۴. | ~E | ∴ E (A.C.P.) |
| ۵. | ~ (B ∨ D) | ۱, ۴, M.T. |
| ۶. | ~~B • ~D | ۵, DeM. |
| ۷. | ~~D • ~B | ۶, Com. |
| ۸. | ~D | ۷, Simp. |
| ۹. | A | ۳, ۸, D.S. |
| ۱۰. | B • C | ۱, ۹, M.P. |
| ۱۱. | B | ۱۰, Simp. |
| ۱۲. | ~B | ۶, Simp. |
| ۱۳. | B • E | ۱۱, Add. |
| ۱۴. | E | ۱۳, ۱۲, D.S. |
| ۱۵. | ~~E ⊃ E | ۴ - ۱۴, C.P. |
| ۱۶ | ~~~E ∨ E | ۵, .Impl |
| ۱۱۷. | E ∨ E | ۱۶, .D.N |
| ۱۱۸. | E | ۱۷, Taut. |
هنگامی که به گزارههای متناقض B (خط ۱۱) و ~B (خط ۱۲) رسیدیم، به سادگی B∨E را با استفاده از افزایش و سپس E، از B∨E و ~B را با کارزدن قیاس فصلی استنتاج می کنیم. ما در اینجا برهان شرطی خود را با خالی کردن فرض خود، با پایان دادن به خط قلمرو، و استنتاج ~E⊃E در خط ۱۵ به پایان میبریم. اما هنوز به نتیجه مطلوب نرسیدهایم، گرچه نزدیک به آن هستیم. با استفاده از استلزام مادی، ~~E∨E را بهدست میآوریم، سپس با نقض دوگانه، E∨E را استنتاج میکنیم، و در نهایت، با قاعده توتولوژی، نتیجه استدلال، یعنی E، را استنتاج میکنیم.
یک برهان غیرمستقیم برای این استدلال، B•~B را در خط ۱۳ استنتاج و سپس این فرض را تخلیه میکند و برهان غیرمستقیم را درسطر ۱۴ با استنتاج نتیجهیِ E کامل میکند. بنابراین، یک برهان غیرمستقیم را میتوان بهعنوان کوتاهسازی یک برهان شرطی در نظر گرفت: در هر دو مورد، یک زیر-برهان اجرا میشود که استنتاج نقیض گزاره فرضشده (یا یک گزاره منطقاً همارز با نقیض آن➥۳۳
۳۳- برهان غیرمستقیم E را پس از تخلیه فرض (یعنی E~) استنتاج میکند، در حالی که برهان شرطی ~E⊃E را استنتاج میکند که منطقاً همارز E است.را امکانپذیر میکند. در تمام موارد مشابه برهانهای غیرمستقیم و جایگزینهای برهان شرطی آنها، برهان شرطی چهار سطر طولانیتر است.
بنابراین، گرچه برهان غیرمستقیم اعتبار با توجه به قوانین نوزده گانه استنتاج و برهان شرطی مورد نیاز واقعی نیست، برهان غیرمستقیم، برهانهای کوتاهتر از برهانهای شرطی متناظر را میسر میکند. به همین دلیل، ما برهان غیرمستقیم را به جعبه ابزار منطقی خود میافزاییم.
ه. نگاه دوبار به برهان شرطی توتولوژیها
برهانهای غیرمستقیمِ توتولوژیها معمولاً کوتاهترین و آسانترین اثباتها برای توتولوژی هستند. با این حال، همانطور که در بند (ه) برهان شرطی میتوان دید، وقتی توتولوژی مورد اثبات، یک گزاره شرطی باشد، برهان شرطی معمولاً کارآمدتر از برهان غیرمستقیم است. برای نمونه، در بند (د)در بالا با کار زدن اپی در ۱۳ سطر ثابت کردیم
[(M ⊃ Q) • M] ⊃ Q
یک توتولوژی است. توتولوژی بودن ای گزاره شرطی با کار زدن برهان شرطی به ۶ سطر نیاز دارد.
| ۱. | (M ⊃ Q) • M | / ∴ Q (A.C.P.) |
| ۲. | M ⊃ Q | ۱, Simp. |
| ۳. | M • (M ⊃ Q) | ۱, Com. |
| ۴. | M | ۳, Simp. |
| ۵. | Q | ۲, 5, M.P. |
| ۶. | [(M ⊃ Q) • M] ⊃ Q | ۱–۵, C.P. |
همینطور،
(Q ⊃ R) ⊃ [(P ⊃ Q) ⊃(P ⊃ R)],
که در ۵ سطر با استفاده از C.P. در بند (ه) برهان شرطی ثابت شد، برای اثبات با I.P. به برهانی ۱۶ سطری نیاز دارد. به خواننده توصیه میشود که خود برهان غیرمستقیم را اجرا کند و دو برهان را با هم مقایسه کند.➥۳۴
و. عبارت-های گزارهای در برهان اعتبار
اکنون که C.P. و I.P. را به جعبه ابزار منطقی خود افزودهایم، میتوانیم به تمام بگوییم که برهان صوری اعتبار، دنبالهای از عبارتهای-گزارهای است که هر یک عبارتند از:
- یک مقدمه،
- یک عبارت-گزارهای که بطور معتبر که از مقدمات اندریافت شده است،
- یک فرض با قلمرو محدود،
- یک عبارت-گزارهای که بطور معتبر درون یک برهان شرطی اندریافت شده، یا است،
- یک عبارت-گزارهای که بطور معتبر درون یک برهان غیرمستقیم اندریافت شده است.
عبارت-گزارهای که در برهان اعتبار با کارزدن C.P. یا I.P. اندریافت میشود - یعنی نتیجهیِ برهان اعتبار C.P. یا I.P. - گزارهای است که بطور معتبر از مقدمات استنتاج میشود.➥۳۵ بنابراین، هر عبارت-گزارهای در برهان اعتبار که در کنار یک خط قلمرو نیست، یا یک مقدمه است یا یک عبارت-گزارهای استنتاجی معتبر از مقدمات است.
